Peramalan Data Runtun Waktu Metode SARIMA dengan Eviews - Hallo sahabat Chord Gitar Indonesia, Pada sharing Kunci gitar kali ini yang berjudul Peramalan Data Runtun Waktu Metode SARIMA dengan Eviews, saya telah menyediakan lirik lagu lengkap dengan kord gitarnya dari awal lagi sampai akhir lagu. mudah-mudahan isi postingan kunci gitar yang saya tulis ini dapat anda pahami. okelah, ini dia chord gitarnya.

Penyanyi : Peramalan Data Runtun Waktu Metode SARIMA dengan Eviews
Judul lagu : Peramalan Data Runtun Waktu Metode SARIMA dengan Eviews

Peramalan Data Runtun Waktu Metode SARIMA dengan Eviews

Portal-Statistik | Malam ini sedang berlangsung bigmatch antara Chelsea VS MU, sambil menunggu kick off babak kedua mending berbagi kepada teman-teman semua...
Setelah kemarin saya berbagi postingan tentang Lankah-langkah Peramalan Dengan Metode ARIMA Box-Jenkins dengan Eviews, malam ini waktunya untuk melanjutkan postingan tentang analisis data runtung waktu metode yang lainnya.
Ya sesuai dengan judul diatas, malam ini saya ingin memberikan sedikit pengetahuan tentang Peramalan Data Runtun Waktu Metode SARIMA (Seasonal Autoregressive Integrated Moving Average) dengan Eviews.


Metode Box-Jenkins
Metode Peramalan adalah cara memperkirakan secara kuantitatif apa yang akan terjadi pada masa yang akan datang, berdasarkan data yang relevan pada masa lalu. Metode ini sangat berguna dalam mengadakan pendekatan analisis terhadap perilaku atau pola dari data yang lalu, sehingga dapat memberikan cara pemikiran, pengerjaan dan pemecahan yang sistematis dan prakmatis serta memberikan tingkat keyakinan yang lebih. Salah satu metode dalam peramalan yaitu metode Box Jenkins. Beberapa model dalam Metode Box-Jenkins yaitu:

1.  Model ARIMA (p,d,q)
   Rumus umum model ARIMA (p,d,q) adalah sebagai berikut
   
   
2. Model ARIMA dan Faktor Musim (SARIMA)
   Notasi ARIMA dapat diperluas untuk menangani aspek musiman, notasi umumnya adalah:
   ARIMA (p,d,q) (P,D,Q)S
   dengan.
   p,d,q         : bagian yang tidak musiman dari model
   (P,D,Q)S   : bagian musiman dari model
   S              : jumlah periode per musim
   Adapun rumus umum dari ARIMA (p,d,q)(P,D,Q)S sebagai berikut :
   
   
3. Stasioneritas data
   Kestasioneran data bisa dilihat dari plot time series. Untuk melihat kestasioneran data dalam means bisa dilihat dari perhitungan ACF dan PACF nya. ACF diperoleh dengan rumus sebagai berikut:
   
   
   

   dengan Zt data time series pada waktu ke t dan Z ̅  rata-rata sampel. Sedangkan PACF diperoleh dengan rumus sebagai berikut:
   

   
   

   dengan ρk adalah fungsi autokorelasi. Ketidakstasioneran data dalam means dapat diatasi dengan proses pembedaan (differencing), sedangkan kestasioneran data dalam varians dapat dilihat dengan nilai λ. Adapun nilai λ dihitung dengan rumus sebagai berikut:
   
   dengan, Yi data aktual untuk i = 1,..., n , G geometric mean dari seluruh data, λ nilai lambda, n jumlah data observasi.

Studi Kasus
Berikut ini adalah data penjualan sepatu sebuah perusahaan A, seorang pemilik perusahaan ingin mengetahui perkembangan penjualannya untuk 1 tahun kedepan guna menentukan sasaran pasar dan kebijakan yang akan diambilnya.
Data dapat diperoleh disini.


Adapun langkah-langkah melakukan forcasting terhadap data dengan menggunakan aplikasi Eviews metode SARIMA adalah.

1. Membuka aplikasi Eviews dengan melakukan double click pada icon desktop atau apalah terserah cara masing-masing.
2.  Setelah aplikasi Eviews terbuka dan siap digunakan, klik menu File – New - Workfile.
   
   
3. Selanjutnya pilih menu Object – New Object, kemudian pilih Series dan isikan nama data pada kotak Name for object.
   
   
4. Selanjutnya double klik pada nama data yang telah dibuat, klik button Edit, dan paste data pada studi kasus pada kolom yang tersedia.
   
   
5. Lihat bentuk data tersebut, klik menu View – Graph – OK.
   
   
6. Karena data tersebut mengandung pola musiman, maka selanjutnya adalah menghilangkan pola musiman tersebut dengan melakukan differencing musiman, klik menu Quick – Generate Series,  pada Enter equation isi dengan kode dslogsepatu=dlog(sepatu,0,12).
   
   
7. Selanjutnya adalah melakukan differencing nonmusiman terhadap data teresebut, klik menu Quick – Generate Series,  pada Enter equation isi dengan kode dslogsepatu=dlog(sepatu).
   
8. Selanjutnya untuk melihat grafik dari hasil differencing musiman dan non musiman tersebut dapat dilakukan dengan select dslogsepatu dan dlogsepatu kemudian klik kanan open – as group,kemudian klik menu View – Graph – OK.
   
9. Sehingga didapatkan hasil seperti gambar dibawah.
   
   
10. Setelah melihat hasil kedua grafik tersebut, langkah selanjutnya adalah melakukan menggabungkan differencing musiman dan nonmusiman tersebut, klik menu Quick – Generate Series,  pada Enter equation isi dengan kode ddslogsepatu=dlog(sepatu,1,12).
    
    
11. Data tersebut telah diasumsikan stasioner terhadap variansi karena telah dilakukan transformasi kedalam bentuk logaritma dan dilakukan differencing musiman dan nonmusiman, selanjutnya adalah menguji apakah data tersebut stasioner terhadap mean, klik menu View – Unit Root Test, kemudian isi sesuai gambar.
    
    
12. Selanjutnya adalah identifikasi model awal, klik menu View – Correlogram, kemudian pilih Ok. Sehingga muncul grafik ACF dan PAC seperti gambar.
    
    
13. Dari model grafik diatas, dapat diduga data tersebut mengikuti model ARIMA(2,1,1)(2,1,1)12. Selanjutnya dilakukan overfitting untuk memilih model yang signifikan dan terbaik. Pada halaman utama Eviews masukkan perintah seperti gambar.
    
    
14. Lakukan overfitting terhadap model-model berikut ini, kemudian tentukan model mana yang signifikan dan terbaik dengan melihat nilai AIC, SC, MSE serta uji asumsi Autokorelasi, Heteroskedasisitas dan Normalitas Residu, untuk melakukan uji normalitas residu, klik menu View – Residual Test – Hostogram Normality Test, selanjutnya adalah uji asumsi autokorelasi, klik menu View – Residual Test – Correlogram Q Statistics, selanjutnya adalah uji asumsi heteroskedastisitas, klik menu View – Residual Test – Correlogram Squared Residuals.
    Tabel Overfitting Model SARIMA
    
15. Selanjutnya adalah melakukan forecast atau peramalan, doubleklik pada range data dan ubah nilai End date dengan 1982M12.
    
    
16. Berdasarkan hasil overfitting tabel diatas, maka yang dipilih adalah model ARIMA(2,1,1)(24,1,12), Klik menu Forecast dan isi sesuai dengan gambar.
    
    
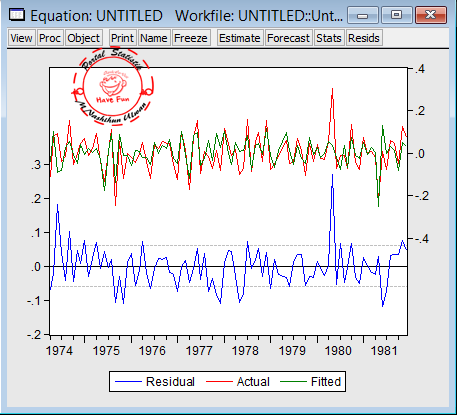
17. Sehingga didapatkanlah hasil forecast dari data tersebut.

PEMBAHASAN

Selanjutnya mari kita bahas satu persatu output hasil dari permalan yang sudah kita lakukan tadi.

 

Berdasarkan gambar, dapat dikatakan bahwa data tersebut mengandung pola musiman yang terus berulang dari tahun ketahun, oleh sebab itu metode yang digunakan dalam melakukan forecast terhadap data tersebut adalah metode SARIMA (Seasonal Autoregressive Integrated Moving Average).
Karena data tersebut mengandung pola musiman, oleh sebab itu dilakukan differencing terhadap pola musiman dan nonmusimannya supaya data statsioner terhadap mean dan variansi.

• Hipotesis
  Ho : Data tidak stasioner
  H1 : Data stasioner
• Tingkat Signifikansi:
   α=0.05
• Daerah Kritis:
  |ADF| >|t-Statistic| : Tolak H0
• Statistika Uji:
  ADF = -13.477        t-Statistic 5% = -2.886
• Keputusan Uji
  Karena nilai |ADF| > |t-Statistic| maka keputusannya adalah tolak H0
• Kesimpulan :
  Jadi dengan tingkat signifikansi 5% didapatkan kesimpulan bahwa data tersebut stasioner terhadap mean.

Setelah data tersebut stasioner terhadap mean dan variansi karena telah dilakukan transformasi dan differencing terhadap pola musiman dan nonmusiman. Selanjutnya adalah pemilihan model terbaik dengan melakukan overfitting.

 

Berdasarkan tabel diatas maka model terbaik yang dapat digunakan adalah model ARIMA (2,1,1)(24,1,12), karenan memiliki nilai AIC, SC, SSR yang paling sedikit serta hasil diagnostic check yang baik:

Berdasarkan gambar, terlihat bahwa nilai Prob. < alpha = 0.000 < 0.05 maka keputusannya adalah tolak H0 yang berarti bahwa data residual tidak berdistribusi normal.

 Berdasarkan gambar diatas terlihat pada nilai prob. semua nilai signifikan (prob. > alpha), oleh karena itu dapat disimpulkan bahwa tidak terdapat gejala autokorelasi terhadap data residual.

Berdasarkan gambar diatas terlihat pada nilai prob. semua nilai signifikan (prob. > alpha), oleh karena itu dapat disimpulkan bahwa tidak terdapat gejala heteroskedastisitas terhadap data residual.

 

 

Gambar diatas merupakan hasil forecast data penjualan sepatu 1 tahun (12 bulan) ke depan, pada gambar pertama dan kedua dapat dilihat informasi RMSE dan MAE yaitu 176.10 dan 152.29, dan pada gambar ketiga dapat dilihat hasil forecast untuk periode 12 bulan kedepan.

Demikian,
Selesai juga ini postingan, sungguh panjang dan sedikit melelahkan,,, hehe.
Jika ada yang kurang jelas silahkan bisa ditanyakan.
Semoga Bermanfaat
HAVE FUN.

Demikianlah Artikel Peramalan Data Runtun Waktu Metode SARIMA dengan Eviews

Sekian Kunci gitar Peramalan Data Runtun Waktu Metode SARIMA dengan Eviews, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, sekian postingan Chord gitar lagu kali ini.

Anda sedang membaca artikel Peramalan Data Runtun Waktu Metode SARIMA dengan Eviews dan artikel ini url permalinknya adalah https://ikazumdammahum.blogspot.com/2014/10/peramalan-data-runtun-waktu-metode.html Semoga artikel ini bisa bermanfaat.

Tweet